Bulk modulus
The bulk modulus (K) of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e. Its base unit is the pascal.[1]
Contents |
Definition
The bulk modulus K>0 can be formally defined by the equation:
where P is pressure, V is volume, and ∂P/∂V denotes the partial derivative of pressure with respect to volume. The inverse of the bulk modulus gives a substance's compressibility.
Other moduli describe the material's response (strain) to other kinds of stress: the shear modulus describes the response to shear, and Young's modulus describes the response to linear stress. For a fluid, only the bulk modulus is meaningful. For an anisotropic solid such as wood or paper, these three moduli do not contain enough information to describe its behaviour, and one must use the full generalized Hooke's law.
Thermodynamic relation
Strictly speaking, the bulk modulus is a thermodynamic quantity, and it is necessary to specify how the temperature varies in order to specify a bulk modulus: constant-temperature (isothermal 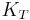 ), constant-entropy (adiabatic
), constant-entropy (adiabatic 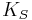 ), and other variations are possible. In practice, such distinctions are usually only relevant for gases.
), and other variations are possible. In practice, such distinctions are usually only relevant for gases.
For a gas, the adiabatic bulk modulus 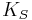 is approximately given by
is approximately given by
and the isothermal bulk modulus 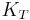 is approximately given by
is approximately given by
where
- γ is the adiabatic index, sometimes called κ.
- P is the pressure.
In a fluid, the bulk modulus K and the density ρ determine the speed of sound c (pressure waves), according to the Newton-Laplace formula
Solids can also sustain transverse waves: for these materials one additional elastic modulus, for example the shear modulus, is needed to determine wave speeds.
Measurement
It is possible to measure the bulk modulus using powder diffraction under applied pressure.
Selected values
| Material | Bulk modulus in GPa | Bulk modulus in ksi |
|---|---|---|
| Glass (see also diagram below table) | 35 to 55 | 5.8×103 |
| Steel | 160 | 23×103 |
| Diamond[2] | 442 | 64×103 |
Material with bulk modulus value of 35GPa needs external pressure of 0.35 GPa (~3500Bar) to reduce the volume by one percent.
| Water | 2.2×109 Pa (value increases at higher pressures) |
| Air | 1.42×105 Pa (adiabatic bulk modulus) |
| Air | 1.01×105 Pa (constant temperature bulk modulus) |
| Solid helium | 5×107 Pa (approximate) |
References
- ^ "Bulk Elastic Properties". hyperphysics. Georgia State University. http://hyperphysics.phy-astr.gsu.edu/hbase/permot3.html.
- ^ Cohen, Marvin (1985). "Calculation of bulk moduli of diamond and zinc-blende solids". Phys. Rev. B 32: 7988–7991. Bibcode 1985PhRvB..32.7988C. doi:10.1103/PhysRevB.32.7988.
- ^ Fluegel, Alexander. "Bulk modulus calculation of glasses". glassproperties.com. http://www.glassproperties.com/bulk_modulus/.
|
|||||
| Conversion formulas | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these, thus given any two, any other of the elastic moduli can be calculated according to these formulas. | ||||||||||
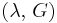 |
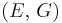 |
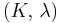 |
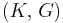 |
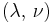 |
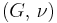 |
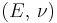 |
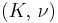 |
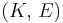 |
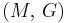 |
|
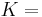 |
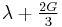 |
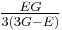 |
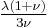 |
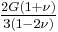 |
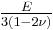 |
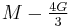 |
||||
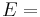 |
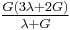 |
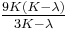 |
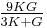 |
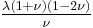 |
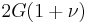 |
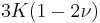 |
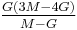 |
|||
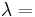 |
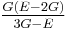 |
 |
 |
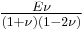 |
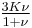 |
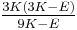 |
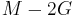 |
|||
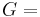 |
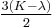 |
 |
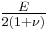 |
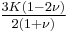 |
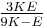 |
|||||
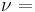 |
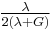 |
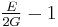 |
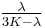 |
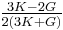 |
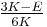 |
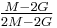 |
||||
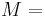 |
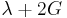 |
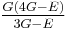 |
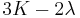 |
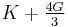 |
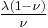 |
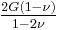 |
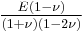 |
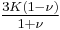 |
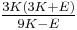 |
|
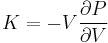
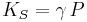
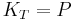
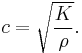
 )
)  )
)  )
)  )
)  )
)  )
)